2020/2/2

2020/2/19
自然界には多くのアイデアが眠っています。 蓮の葉から水をはじく構造のヒントを得たとか、オナモミからマジックテープのヒントを得たとか、有名な話だと思います。 群知能もそんな風に自然界から着想された一つです。 群知能とは「鳥の群れのように個体間の局所的な関係を合わせて、集団として高度な動きを見せる現象を模した計算手法」です。 粒子群最適化(PSO)や蟻コロニー最適化(ACO)などいろいろありますが、今回は人工蜂コロニーアルゴリズム(artificial bee colony algorhythm , 以下ABCと表記)について実装します。
収穫蜂(employed bee)、追従蜂(onlooker bee)、偵察蜂(scout bee)の3つの種類の蜂の動きを模した操作で探索点を更新していきます。
収穫蜂\(N\)匹をアルゴリズムを適応する空間(\(D\)次元)にランダムに初期配置する。 全ての収穫蜂に対してカウンタ\(TC\)というものをそれぞれ定義し、初期値0にしておく。
収穫蜂\(i\)について順番に次の更新式で探索点を更新していく。
\[ v_{ij} = x_{ij} + r_{ij}(x_{ij}-x_{kj}) \]ただし、\(i=1\sim N\)は収穫蜂の個体番号、\(j=1\sim D\)は次元、\(k=1\sim N(k\neq i)\)は\(i\)とは異なる収穫蜂の個体番号であり、\(j,k\)についてはランダムにそれぞれ一つの値を選ぶ。 また、\(r_{ij}\)は\(-1\)から\(1\)の一様乱数である。\(v_{i}\)は収穫蜂\(i\)の新たな探索点候補、\(x_{i}\)は現在の探索点を表す。
このとき新探索点候補が現在の探索点より適合度\(f\)が高ければ(最小値問題なら関数値が小さければ)、探索点を更新しカウンタを0にする。 反対に現在の探索点の方が適合度が高ければ更新はせず代わりにカウンタを+1する。 数式で書くと以下のようになる。
\begin{align*} x_i = \begin{cases} v_i & if \quad f_{v_i}>f_{x_i} & then \quad TC_i = 0\\ x_i & otherwise & then \quad TC_i = TC_i + 1 \end{cases} \end{align*}
追従蜂N匹を使ってさらに探索を進める。
追従蜂は、以下のように求められる確率を使って収穫蜂1匹をルーレット選択し、Step1の作業を行う。
この作業を全ての追従蜂について繰り返す。
カウンタ\(TC\)があらかじめ設定した閾値を超えている場合、その収穫蜂の探索点を初期化する。
Step1〜3を規定回数行ったら終了とする。(あるいはあらかじめ決めておいた終了条件を満たした、などでも良い)
探索の中で見つかった最良の探索点が近似解です。 収穫蜂が最初に蜜を探しに出かけて、追従蜂が優秀な収穫蜂の近くを探索して、偵察蜂があまりに役立たずな収穫蜂を粛清する、といったイメージでしょうか。 偵察蜂は収穫蜂が局所解にハマって抜け出せないことを防ぎます。
Pythonで実装してみます。
今回は2次元のsphere関数\( (z = x^2 + y^2,-5 < x < 5 ,-5 < y < 5) \)の最小値を求めることにします。
適合度として
\begin{align*}
f(z_i) = \begin{cases}
\dfrac{1}{1+z_i} & if \quad z_i > 0\\
1+|z_i| & otherwise
\end{cases}
\end{align*}
を設定します。こうすることで、関数値が小さいほど適合度は高くなります。
[コードを表示]
Python
import numpy as np
import matplotlib.pyplot as plt
import math
# 関数の設定
# xはndarray
# sphere
def func(x):
return np.sum(x**2)
# rastrigin
# def func(x):
# s = 0
# for i in range(len(x)):
# s += x[i]**2 - 10*math.cos(2*math.pi*x[i])
# return 10*d + s
# 初期設定
N = 100 # 収穫蜂と追従蜂の個体数
d = 2 # 次元
TC = np.zeros(N) #更新カウント
lim = 30
xmax = 5
xmin = -5
G = 100 # 繰り返す回数
x = np.zeros((N,d))
for i in range(N):
x[i] = (xmax-xmin)*np.random.rand(d) + xmin
def fit(x):
z = func(x)
if z > 0:
return 1/(1+z)
else: return 1+abs(z)
# ルーレット選択用関数
def roulette_choice(w):
tot = []
acc = 0
for e in w:
acc += e
tot.append(acc)
r = np.random.random() * acc
for i, e in enumerate(tot):
if r <= e:
return i
x_best = [0,0] #x_bestの初期化
best = 100
# 繰り返し
best_value = []
ims = []
for g in range(G):
best_value.append(best)
z = np.zeros(N)
for i in range(N):
z[i] = func(x[i])
# employee bee step
for i in range(N):
v = x.copy()
k = i
while k == i:
k = np.random.randint(N)
j = np.random.randint(d)
r = np.random.rand()*2 - 1 # -1から1までの一様乱数
v[i,j] = x[i,j] + r * (x[i,j] - x[k,j])
if fit(x[i]) < fit(v[i]):
x[i] = v[i]
TC[i] = 0
else: TC[i] += 1
# onlooker bee step
w = []
for i in range(N):
w.append(fit(x[i]))
for l in range(N):
i = roulette_choice(w)
j = np.random.randint(d)
r = np.random.rand()*2 - 1 # -1から1までの一様乱数
v[i,j] = x[i,j] + r * (x[i,j] - x[k,j])
if fit(x[i]) < fit(v[i]):
x[i] = v[i]
TC[i] = 0
else: TC[i] += 1
# scout bee step
for i in range(N):
if TC[i] > lim:
for j in range(d):
x[i,j] = np.random.rand()*(xmax-xmin) + xmin
TC[i] = 0
# 最良個体の発見
for i in range(N):
if best > func(x[i]):
x_best = x[i].copy()
best = func(x[i])
# 結果
print("発見した最小値:{}\nそのときのx:{}".format(func(x_best),x_best))
plt.plot(range(len(best_value)),best_value)
plt.yscale('log')
plt.title("Sphere")
plt.xlabel("試行回数")
plt.ylabel("発見した最小値")
plt.show()
実行結果は毎回変わりますが、例えば以下のようになります。
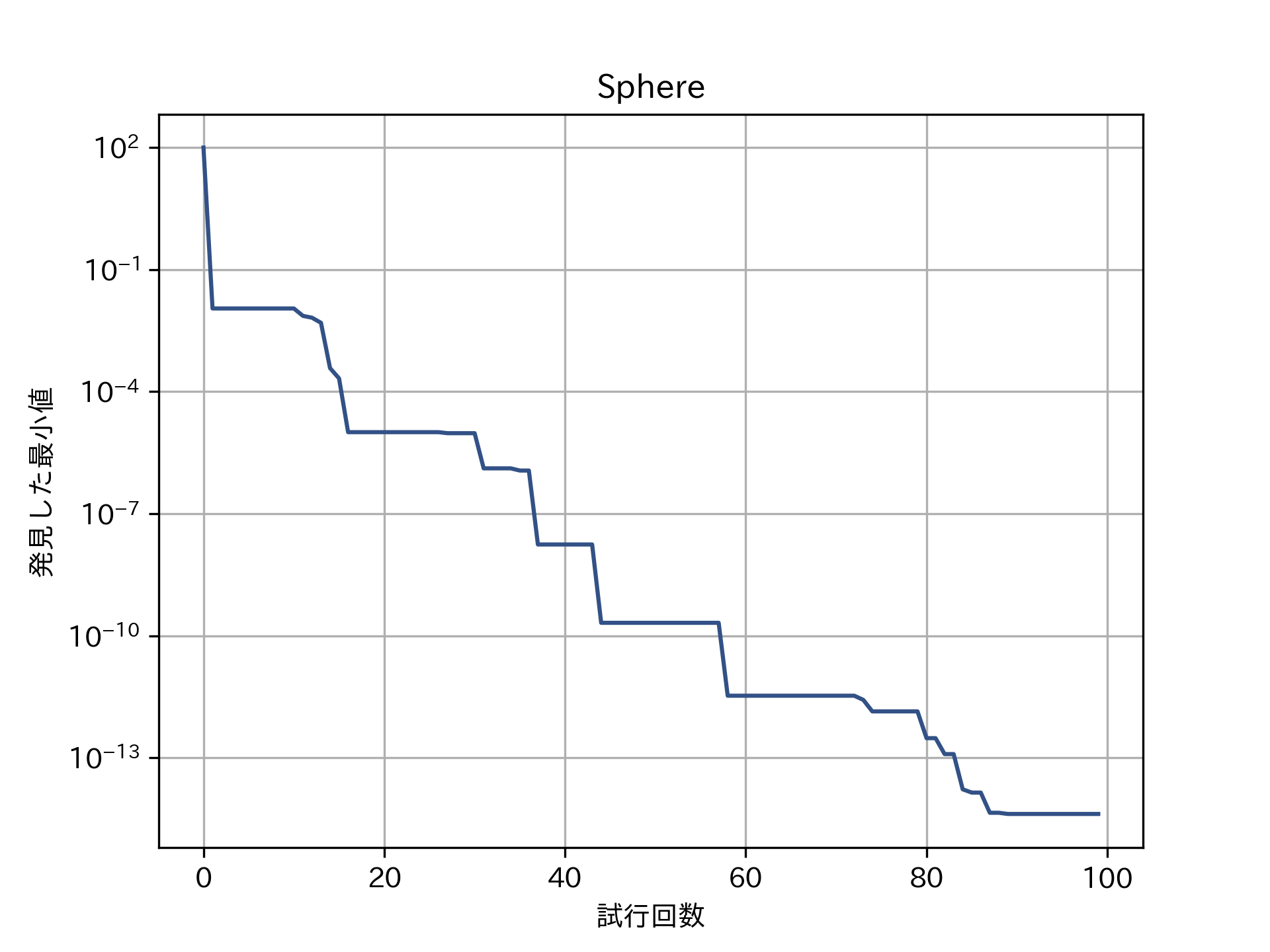
試行回数を重ねるごとにより小さい関数値を発見できていることがわかります。
有効数字二桁で表すと\((x,y)=(-5.3\times 10^{-8}, -1.41\times 10^{-9})\)のときに最小値\(2.77\times 10^{-15}\)を取ると出てきます。
つまり、ほぼ原点で最小値ほぼ0を取るということです。
このように、ABCは数学的に厳密に正しい答えを求めるというよりはあくまで近似解を求めるアルゴリズムです。 解析的に解を求められないような問題に役立ちます。 どのように蜂たちが動いているのかもう少し見てみます。



だんだんと点が(0,0)に集まっていっているのがわかります。 しかし、このような簡単な関数に対してであれば解析的にも最小値は求められます。 特にABCを使う利点はありません。 では、他の関数はどうでしょうか。 Rastrigin関数という多峰性関数について見てみます。
\begin{align*} z(x_1,x_2,\cdots,x_d) = 10d + \sum_{i=1}^d \left[ x_i^2 - 10\cos(2\pi x_i)\right]\\ min\hspace{1mm}z(x_1,x_2,\cdots,x_d)=0\quad(x_1,x_2,\cdots,x_d=0) \end{align*}

(出典:Wikipedia) こんな感じで極小値が多い関数となっています。 例えば勾配法のような方法だと最小値を探索するのが難しそうです。 これについてABCで最小値探索をしてみると

\((x,y)=(-1.77\times 10^{-7}, -1.50\times 10^{-5})\)のとき最小値\(4.49\times 10^{-8}\)をとる、という計算結果が出ました。
このように探索が難しそうな関数に対しても安定して近似解を見つけることができているようです。
今回のまとめ
参考
前田陽一郎(2018):“人工蜂コロニーアルゴリズムのためのハイブリッド探索手法”, 知能と情報(日本知能情報ファジィ学会誌), 30(2), pp.556–563
森大輔,山口智(2013):“主成分分析を取り入れた Artificial Bee Colony アルゴリズム”, 電気学会論文誌C,135(4), pp.423-435